2023 – High-Performance Optimization, Backpropagation, Quantum Computing
Research, Native (C++)
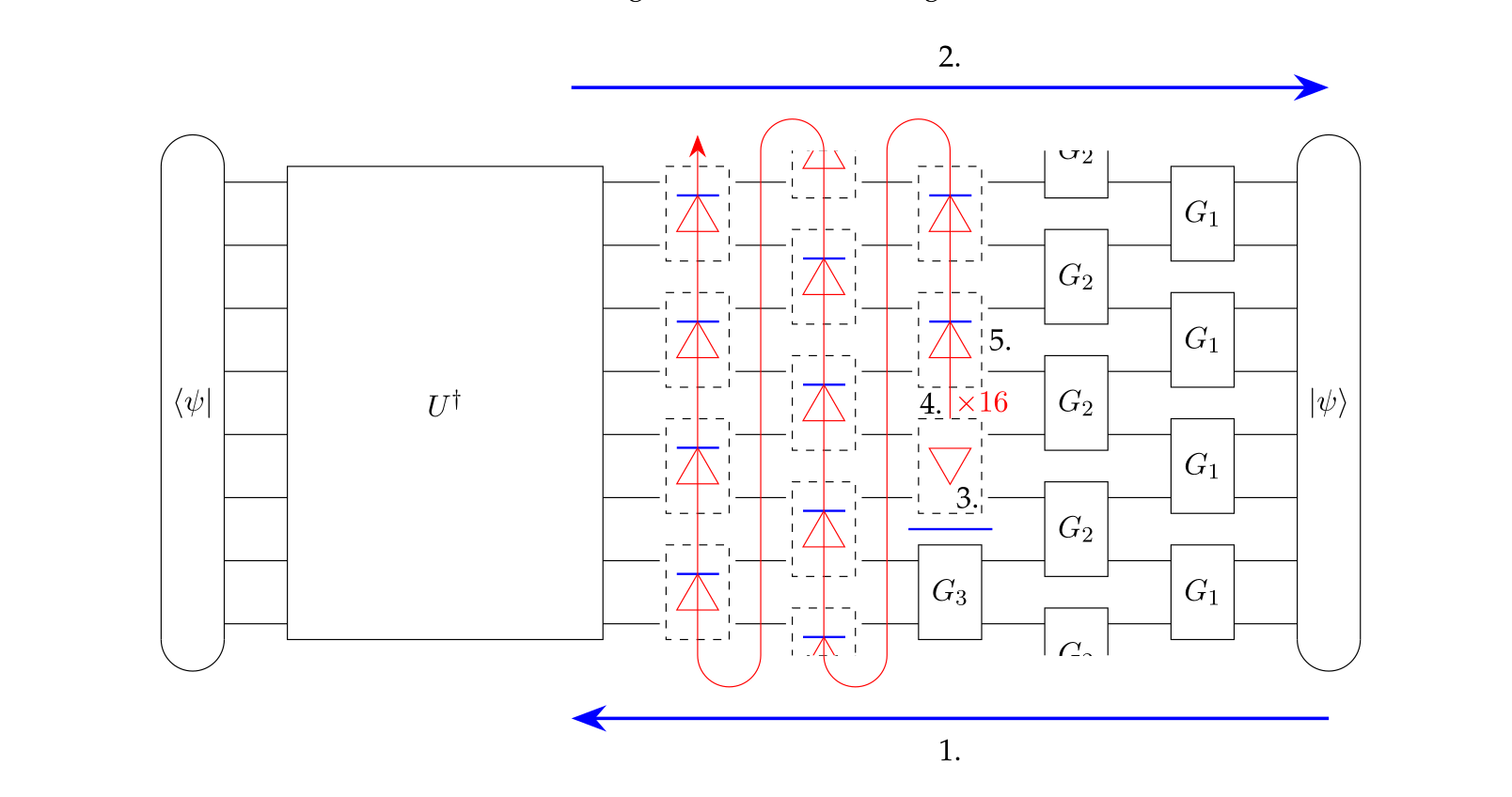
High Performance Contraction of Brickwall Quantum
Circuits for Riemannian Optimization
Quantum computers show a lot of promise in enabling the large-scale computational workloads of the future. Their capability scales exponentially with the number of qubits used. Due to this property, they are well suited for Hamiltonian simulation, the simulation of quantum processes itself scaling exponentially.
Various solutions for building a quantum circuit for this purpose exist. Those are not suitable for error-prone systems of the NISQ area though. One possible mitigation for this problem is shortening the circuit by using Riemannian optimization. This works well for 1-dimensional systems but breaks down when looking at larger 2-dimensional cases as the complexity of the classical method scales exponentially with the qubit count. Applying it therefore requires efficient brickwall tensor network contraction as well as gradient and Hessian computation performance and memory-wise. Existing methods for contraction and the similar problem of deep learning fail to exploit the specific constrained structure of the given brickwall and thereby fall short of solving the problem quickly.
This thesis investigates whether brickwall tensor network contraction can be optimized sufficiently to be run in a reasonable time frame. Algorithms for the various subtasks such as gradient and Hessian computation are proposed. A native implementation of those is provided, tested for correctness, and evaluated for performance improvements.
The largest gain is achieved by applying the tensor network to all 1-hot state vectors gate-wise instead of performing a contraction of the layer matrices. The other major improvement is using caching to store intermediate results. The performance of the gradient is increased by a factor of 30, that of the Hessian by 10. The memory requirement is reduced from at least 72 GB to less than 2 GB. The efficiency is L3 cache-bound but given enough space on a server processor scales well with parallelization over cores and distribution over multiple nodes.
Using the algorithms developed in this work on a compute cluster, obtaining the gradients and Hessians required for the Riemannian quantum circuit optimization is possible significantly faster in a matter of weeks rather than years.